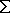 C
i X
i
C
i X
isubject to:
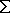 Q
iX
i
Q
iX
i  M
M
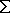 N
iQ
iX
i
N
iQ
iX
i  L
L
X i
 T (i=1,...,15)
T (i=1,...,15)Z, C, X, Q, N, T
 0
0
The City of Azul (Buenos Aires Province, Argentina), as many small cities in the country, is supplied entirely by local groundwater. Such waters contain variable, but generally high concentrations of N-NO3, which hinder their use. This situation, however, has not been addressed, either by local officials or by the affected users. This paper shows that water quality degradation is of man-made origin and affects mainly the urban area where the supply wells are located. Three alternatives directed towards solving or ameliorating the problem are proposed: water treatment, water blending by drilling new wells in nearby, non-polluted zones, and optimization of the current supply system (a battery of 15 wells). The latter solution-posed as a linear optimization problem- is shown to be the least-cost solution because it: (a) does not require additional investments, (b) satisfies the average daily water demand, (c) leads to supply waters carrying at most 45 mg/l of N-NO3 (the maximum allowable concentration set by federal water authorities), and (d) allows for a shut-off time of 6 hours at each pumping well for maintenance purposes.
INTRODUCTION
Many small cities in Argentina rely on groundwater pumping to cover their daily supply of potable water. Other data (CONAPA, 1991) indicate that only 37% of cities have sewage disposal systems. These facts highlight the need to establish severe quality controls for the water supplied.
The city of Azul (Buenos Aires Province, Argentina) constitutes a clear example of this rather risky situation: the water supply is provided by a battery of wells of variable depth which pump water from a regional phreatic aquifer. Many of these wells extract waters carrying a high content of N-NO3, whose origin can be related to partially sewered city sectors with high population densities. It should be noted that groundwater levels are very close to the surface, between a few decimeters and 3 meters. So far, the water supply objective is to cover the water demand at all times, without paying much attention to quality-related issues (e.g., not surpassing the allowable N-NO3 concentration of 45 mg/l). Moreover, public opinion is mistakenly oriented to statements of the type "If nothing has happened for so many years, why should we worry about it?" or "What else can be done when N-NO3 is everywhere?".
This paper, which summarizes the results of several months of field surveying and data processing, pursues two goals, namely, (1) to demonstrate that N-NO3 pollution has a clear man-made origin and that it is areally restricted, and (2) to propose modifications of the pumping regime/schedule for assessing the quantity/quality problems of the local water supply.
HYDROCHEMICAL CHARACTERIZATION
A groundwater sampling survey was carried out in 1991, which was designed to diagnose the water quality status in and around the city of Azul (Figure 1). Samples were obtained at 51 locations, of which 20 are upstream and downstream of the city and the remaining 31 are withinthe city limits (3 of those 51 samples correspond to Azul Creek). The chemical variables, measured by standard methods (APHA, AWWA, WPCF, 1989) were the concentration of Ca, Mg, Na, K, Cl, SO4, N-NO3, CO3 and HCO3, as well as electrical conductivity, dry residue, pH and temperature. The analytical results were subject to a number of tests in order to minimize errors in the mass balance (less than 5% in all cases).
Groundwaters from both sectors (city and rural) were of the bicarbonate-sodium type, although there were differences in the relative and absolute concentrations of other chemical species. City waters have higher TDS (total dissolved solids), mainly due to increased concentrations of sodium, chloride, nitrate-nitrogen, and sulfate. As a summary, Table 1 presents the main statistical parameters of most of the chemical constituents measured.
The areal distribution of the chemical variables (not shown) confirms that, in the rural zone, their concentrations are generally lower with respect to the city water and more evenly distributed. In order to have an additional diagnostic tool, the data set was subject to Q-mode principal components analysis (Harman, 1976), which is aimed at detecting relationships among the samples based on their chemical characteristics. After Varimax (i.e., rigid) rotation, two principal components (PC) were able to justify 99.73% of the variance embedded in the data. PC1 explained 51.17% of the variance, whereas PC2 took over the remaining 48.56%. The results are graphically displayed in Figure 2.
The discrimination achieved is strikingly clear: rural waters and city waters can be considered as pure members of different characteristics; the overlap at the center of Figure 2 corresponds to samples close to the city limits; additionally, waters of the Azul Creek are similar to those found in the rural zone. That does not necessarily mean that mixing of waters of different origin is being postulated. It is, rather, the consequence of man-made degrading factors acting on an unique type of water along its natural flow path.
Table 1. Mean (m) and standard deviation (s) of analytical data. All values are in mg/l but Electrical Conductivity (E.C.), whose units are micromhos/cm at 25 oC.
| Samples from the urban domain (n=31) | |||||||||
| Ca | Mg | Na | K | Cl | NO3 | SO4 | HCO3 | E.C. | |
| m | 44 | 17 | 164 | 11 | 77 | 39 | 50 | 443 | 1256 |
| s | 21 | 13 | 30 | 4 | 52 | 33 | 18 | 102 | 249 |
| Samples from the rural domain (n=20) | |||||||||
| m | 42 | 21 | 126 | 10 | 30 | 24 | 16 | 502 | 847 |
| s | 17 | 11 | 52 | 4 | 10 | 15 | 20 | 84 | 232 |
MANAGEMENT ALTERNATIVES
Having determined that the chemistry of the local groundwaters do not share common characteristics and that at least two major zones can be seen (city waters and the rest), the next step was directed towards proposing plausible management alternatives of the quantitative and qualitative aspects of the city water supply.
Inasmuch as N-NO3 is not a toxic substance and is harmless as long as its concentration is less or equal than 45 mg/l, the alternatives presented below are governed by a common economic objective: the existing battery of wells cannot be relocated nor it can be put out of operation; it can, however, be supplemented with waters with low N-NO3 content, or its operational characteristics be changed so that the supplied water contains less than 45 mg/l of N-NO3.
Water treatment
Cost-related issues of water treatment can be inferred from an example taken from Lauch and Guter (1985). McFarland City (California,USA), a community of 6000 inhabitants, had to be supplied with waters from a local aquifer (only source of water) severely contaminated with N-NO3. The cost of drilling a well to a depth free of contamination was similar to installing a treatment plant of 3785 m3/day. Treatment was selected with a total cost of 0.06 $/m3 (capital + operation + maintenance). If that figure is considered as valid for the case of Azul City (average daily supply of 18850 m3), the treatment cost would be 1131 $/day, which is comparable to the current cost of energy needed to drive the pumping system. A one to one extrapolation is made, which is on the safe side because, as the volume of treated water increases, the unit cost of such treatment is expected to decrease.
The figures above should be considered a very conservative scenario because the implicit assumption is that all pumped water is to be treated. Actually, it would only be important to treat the water from those wells containing more than 45 mg/l of N-NO3, which would substantially lower the total cost. This example constitutes an exercise which, eventually, is to be fine-tuned. It is useful, however, to demonstrate that the solution is technically possible and economically feasible.
Water blending
The possibility of deepening the existing wells was not considered because, due to vertical migration from the upper section of the highly contaminated aquifer, even water pumped from a depth of 80 m contains appreciable amounts of N-NO3. On the other hand, deepening cannot proceed much because the bedrock is at a depth ranging from about 100 to 120 m. However, several sectors within the city have been identified with N-NO3 concentrations in the order of 15 to 20 mg/l. Moreover, those sectors are not far away from the central distribution system. Therefore, it would only be necessary to drill two or three wells (total cost about $ 2000/well), whose waters can be mixed with those coming from the other wells in such a way that the final N-NO3 is less than 45 mg/l.
Supply system optimization
This is the least-cost alternative and, as such, deserves special attention. The existing water supply relies on 15 wells, of varying N-NO3 concentrations, whose operation is not organized. The goal is to satisfy the water demand at all times and, in pursuing it, pumping wells are activated or deactivated arbitrarily. Two negative facts emerge from such an operation: the final N-NO3 concentration of the water supplied can vary between previously unpredictable broad ranges, and some wells work 24 hours a day while others remain idle for long periods.
The proposed optimization is based on four constraints, namely, (1) to satisfy the average daily demand, (2) to supply waters with N-NO3 less than 45 mg/l, (3) to minimize the electrical energy needed to drive the well pumps, and (4) to limit the pumping time so as to allow a regular maintenance of the pumps and wells.
The raw data consisted of numerous chemical analyses of the water pumped at the 15 wells since 1968 (shown in Table 2), the daily water demand for the period 1989-1991, the nominal discharge of each well, and the electrical energy consumed by each well.
The problem was posed as one falling in the realm of linear programming. The algorithm used wasthe widely known simplex (Haith, 1982), as implemented by the digital code LINDO (Lindo Systems, 1984). Given an objective function (Z), which expresses mathematically the main goal pursued, the model is as follows:
| Well number | Number of chemical analyses available | Maximum concentration (mg/l) | Minimum concentration (mg/l) | Average concentration (mg/l) |
| 1 | 90 | 57 | 3 | 13 |
| 2 | 66 | 36 | 1 | 10 |
| 3 | 87 | 92 | 9 | 30 |
| 4 | 98 | 140 | 18 | 75 |
| 5 | 60 | 155 | 13 | 62 |
| 6 | 84 | 165 | 38 | 82 |
| 7 | 91 | 168 | 8 | 48 |
| 8 | 55 | 140 | 22 | 71 |
| 9 | 74 | 215 | 26 | 59 |
| 10 | 72 | 182 | 40 | 122 |
| 11 | 30 | 65 | 13 | 40 |
| 12 | 2 | 63 | 56 | 59 |
| 13 | 4 | 240 | 33 | 105 |
| 14 | 2 | 20 | 8 | 14 |
| 15 | 2 | 30 | 2 | 16 |
min Z = 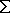 C
i X
i
C
i X
i
subject to:
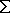 Q
iX
i
Q
iX
i  M
M
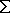 N
iQ
iX
i
N
iQ
iX
i  L
L
X
i  T (i=1,...,15)
T (i=1,...,15)
Z, C, X, Q, N, T  0
0
where:
Z: daily energy consumption by all pumping wells (kW/day),
Ci: energy used by well i (kW/hour),
Xi: pumping period of well i (hours),
Qi: discharge at well i (m3/hour),
M: total daily water demand (m3),
Ni: N-NO3
content of waters pumped at well i (mg/m3),
L: maximum allowable N-NO3
content for the total daily water demand (mg),
T: maximum period of pumping (hours)
T was set to 18 hours after consulting technical personnel who deemed that 6 hours per day would be enough for a regular maintenance program, whereas the value for L was calculated taking into consideration the N-NO3 limit of 45 mg/l according to the following expression: L = 45 mg/l * 1000 l/m3 * M.
Results of the optimization are shown in Table 3. As expected, a global minimum in terms of energy consumption corresponds to a water supply which contains exactly the maximum allowable N-NO3 concentration. Note that two wells (6 and 10) should be shut off.
| Objective function value: 4918.50 kW | |||
| Well number | Pumping period (h) | Well number | Pumping period (h) |
| 1 | 18.00 | 9 | 18.00 |
| 2 | 18.00 | 10 | 0.00 |
| 3 | 18.00 | 11 | 18.00 |
| 4 | 18.00 | 12 | 18.00 |
| 5 | 18.00 | 13 | 2.20 |
| 6 | 0.00 | 14 | 18.00 |
| 7 | 18.00 | 15 | 18.00 |
| 8 | 15.72 | ||
As only the average daily demand has been used throughout, it appeared important to extend the calculations to a broad range of daily water demands, which is realistic in the sense that some fluctuations around the mean value should be expected according to particular seasons in the year. Such computations are shown in Figure 3, which includes the information of the current pumping costs for comparison purposes. Notice that for daily water demands smaller than 17000 m3 the estimated curve is below the current power consumption (i.e., the optimization led to lower costs), whereas for demands between 17000 and 19000 m3/day costs are similar.
On the other hand, if one considers the high variability in the concentrations of N-NO3 already reported (Table 2), it is not possible to postulate a model based only on the mean N-NO3 content at each well. In order to address that, new optmizations were tried at different daily demands considering N-NO3 concentrations which were set plus and minus one standard deviation (S.D.) from their respective means (x) at each well. From Figure 3, it is seen that the curve for x+(1 S.D.) can comply with the limiting equations for demands up to 12000 m3/day, whereas the x-(1S.D.) curve is always below the current costs.
CONCLUSIONS
The distribution of chemical species in the surveyed area, along with the results of a principal components analysis, demonstrate quite clearly that the quality of Azul City groundwater differs from that of the surrounding rural zone. The observed worsening in the city can only be attributed to man-made actions. This should be highlighted because it is precisely within the city that water supply wells are located. The current status as far as N-NO3 concentrations in the water supply cannot be sustained much longer. Out of the three management alternatives presented, two of them imply relevant infrastructural investments. Changing the current operational scheme, however, would not signify any economical sacrifice and, as long as there is a central water storage facility, it would only require making a decision and a little training of personnel. The rewards are not trivial: water demand will always be satisfied, the supplied water will not contain more than 45 mg/l of N-NO3, and some basic system maintenance issues will be addressed.
Acknowledgements: The authors wish to give their sincere thanks to three colleagues who kindly agreed to review the manuscript and suggested valuable modifications and much needed clarifications.
REFERENCES
APHA, AWWA, WPCF, Métodos Normalizados Para el Análisis de Aguas Potables y Residuales, 17th Ed. Ediciones Díaz de Santos S.A., 1989.
CONAPA; Informe Nacional a la Conferencia Sobre Medio Ambiente y Desarrollo de las Naciones Unidas. Comisión Nacional de Política Ambiental, 583 p., 1991.
Haith, D., Environmental Systems Optimization. John Wiley and Sons, 306 p., 1982.
Harman, H., Modern Factor Analysis, 3rd Edition Revised, The University of Chicago Press, Chicago, 1976, 487 p.
Lauch, R. and G. Guter, A one MGD exchange plant for removal of nitrate from well water. Proceedings of the 5th National Symposium and Exposition on Aquifer Restoration and Ground Water Monitoring, pp. 546-570, 1985.
Lindo Systems, Linear Interactive and Discrete Optimizer - PC Version. Lindo Systems, 1984.
Eduardo Usunoff or Marcelo Varni
Instituto de Hidrología de Llanuras
Intendente Giraut s/n
Casilla de Correo 178
(7300) Azul - Provincia de Buenos Aires
Argentina
Phone/Fax: +54 -281-32666
Email:ihlla@uncagr.edu.ar
 Return to HydroWeb Homepage
Return to HydroWeb Homepage