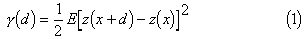
Shakeel AHMED, S. SANKARAN and C.P. GUPTA
National Geophysical Research Institute, Hyderabad-500007, India
ABSTRACT
Geostatistical analysis of some of the hydrogeological parameters viz., transmissivity, water level, and depth to the aquifer basement, has been carried out for an aquifer in the Vaippar basin in a weathered hard rock area. The analysis took into account the geological features such as lineaments, which significantly control groundwater movement. Accordingly the study area was divided into a number of zones based on the density of the lineaments visible on an air photo map. The mean as well as zonal variograms for the three parameters were computed and analyzed with respect to variogram parameters sill, range and others. The study reveals that geostatistical analysis of data for an aquifer should be done by dividing the system into a number of zones and hence the estimation before assigning the parameters to each node of the model. It is also seen that anisotropy plays an important role which should not be ignored by assuming the system to be isotropic.
INTRODUCTION
Management of groundwater resources requires a quantitative estimate of the response of an aquifer system to different input/output stresses enabling one to choose optimal hazard-free development plans. Predictive aquifer modeling can help accomplish this objective provided, of course, the model is properly calibrated.
Quite often, however, geohydrological data which forms the basis of a conceptual aquifer model is quite sparse. This necessitates the modeller to "guestimate" a number of parametric values and modify them in the process of model calibration through a "trial and error" method. It is essential to take into consideration the geology of the area which plays a vital role in parameter variability and groundwater movement. Due to constraints of cost and feasibility, parameters cannot be measured at as large a number of locations as may be required by an aquifer model. Therefore, it is inevitable that various parameters must be estimated at the unmeasured locations from the measured and interpreted values.
The important hydrogeological parameters including hydraulic head, transmissivity, aquifer thickness, storage coefficient, rainfall, and effective recharge are all functions of space and are very often highly variable (Ahmed, 1985). However, this variability is, in general, not purely random. If measurements are made at two different locations, the closer the points of measurement, the closer are the measured values. In other words there is some kind of correlation in the spatial distribution of these parameters. Matheron (1971) has given the name "regionalized variable" to these types of parameters. The autocorrelation of these parameters depends highly on the continuity of the system and hence is affected by the geological structures which control the movement of groundwater. Kriging, an estimator of these regionalized variables, is a potential tool in increasing the accuracy of the model calibration as it provides the best estimates of the system parameters together with an error of estimation.
Usually, however, geo-statistical analysis is carried out using only quantitative data whereas qualitative geological information is often neglected (Aboufirassi and Marino, 1984, Ahmed et al., 1991). This approach has, therefore, been adopted in variogram analysis in the present work.
ABOUT VARIOGRAMS
Hydrogeological parameters often show random variations. However, as they are the result of certain physical processes, correlations of varying degree are obvious. Essentially, estimation of a regionalized variable is to calculate the variability of the parameter. Two common functions, covariance and variogram, which are based on different hypotheses, are calculated for the variographic analysis of a variable using statistical methods. The variogram is however, calculated based on a less restrictive hypothesis and hence is applicable for most of the hydrogeological parameters. The analytical equation to compute a variogram from the field data of any variable (say Z) is as follows:
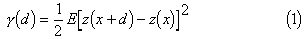
where the function  (d) is the
variogram (also called semi-variogram) between the two points, d
distance apart; z(x) and z(x+d) are the pair of field values of
the parameter Z at x and x+d respectively.
E represents the expected value. The variogram is also calculated in different
directions by taking the pairs in that particular direction only.
However, in practice the variograms can be calculated using the
following formula (Ahmed, 1989).
(d) is the
variogram (also called semi-variogram) between the two points, d
distance apart; z(x) and z(x+d) are the pair of field values of
the parameter Z at x and x+d respectively.
E represents the expected value. The variogram is also calculated in different
directions by taking the pairs in that particular direction only.
However, in practice the variograms can be calculated using the
following formula (Ahmed, 1989).
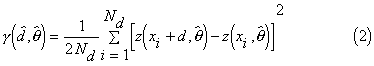
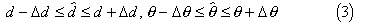
and
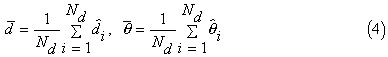
where d and  are the chosen lag and direction of the variogram
respectively.
are the chosen lag and direction of the variogram
respectively. 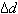 and
and  are tolerance on lag and direction
respectively.
are tolerance on lag and direction
respectively. 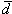 and
and  are the actual lag and direction for the
corresponding calculated variogram. Nd
is the number of pairs for a particular lag and direction.
are the actual lag and direction for the
corresponding calculated variogram. Nd
is the number of pairs for a particular lag and direction.
An experimental variogram is usually an irregular curve due to large value of lag and tolerance. It is, therefore, modelled with smooth functions having three parameters viz., sill, range and the nugget effect (Marsily, 1986 and Marsily and Ahmed, 1987). The transmissivity variogram often shows a nugget effect whereas the water level does not.
A variogram being a square function, is always positive starting from the origin. It attains a maximum value or sill after a certain distance, or lag, which is called the range. However, sometimes due to high variability, a sudden rise appears very near to the origin. Due to lack of close sampling an extrapolation of the variogram towards y-axis can be made and the intercept is called the nugget effect. The computed experimental variograms were analyzed for these properties.
ABOUT THE AQUIFER STUDIED
A model of the aquifer system in Vaippar basin was constructed. The aquifer is unconfined comprising weathered and part of the fractured zones. The area is located in the south-western portion of Ramanathapuram and northern portion of Tirunelveli districts of Tamilnadu, India. It covers an area of 1700 km2 between the latitude 9deg 9min 5sec N to 9deg 32min 25sec N and longitude 77deg 23min 40sec E to 78deg 1min 25sec E. (Figure 1). The area is mainly drained by the Vaippar river. A major portion of the basin is covered by crystalline rocks of archean age consisting of granitic gneisses and charnokites (Gupta and Sankaran, 1986). The bore wells drilled by the Tamilnadu Public Works Department (Groundwater Wing) tap only the weathered zone except for a few deeper wells. The location of wells for monitoring water levels and transmissivity values are shown in Figure 2.
COMPUTATION OF EXPERIMENTAL VARIOGRAMS
The modeling study was handicapped by the sparsity of data. A variographic analysis was, therefore, carried out to estimate transmissivity, water levels and depth to the basement of the aquifer at the unmeasured locations. However, this was not in a purely statistical manner but the area was divided into a number of zones depending upon the density of lineaments. Different zones, A, B, C, D and E, are shown in Figure 2. The area was divided into these five different zones in two steps. In the first step it was divided into 2 zones, A and B. A has no lineaments and B has two groups of lineaments. In the second step the area was divided into three zones, C, D and E. C is free from lineaments, B has one group of lineaments and E has another group of lineaments. The number of measured values available in different zones is given in Table 1.
Eighteen mean variograms (average for the area as well as zone) and four directional variograms were calculated with appropriate lag and tolerance for the three parameters using the software "PLAYG" (Ahmed 1993).
VARIOGRAPHIC ANALYSIS
The experimental variograms calculated for the water table in different zones, are shown in Figures 3 A, B, C, D and E. Water levels being a non-stationary variable, all the variograms show ascending trends without stabilizing around a particular value. A drift calculation has to be made to calculate the variograms of the residuals. However, the slope of the variograms near the origin is very gentle confirming the continuity of the flow system and absence of any discontinuity (for zones A and C, Figures 3 A and 3 respectively). Moreover, variograms calculated in zones B, D and E are comparatively less smooth near the origin confirming the presence of irregular structures.
Directional variograms (Figures 4 B and C) have been calculated in two directions i.e. 20 degrees and 110 degrees from the x-axis (assuming 110 degrees to be the average flow direction). It shows that the variograms in the direction 110 degrees is smoother than the one in the direction 20 degrees. The variograms calculated in the direction 20 dgrees have to take pairs of water-level measurement across the lineaments giving rise to a high variability and low correlation. The high variability and irregularity at the origin show the effect of these geological structures because variability is low in general in the direction perpendicular to the flow direction.
Table 1.
|
Zones |
Transmi ssivity | Water level | Depth to Basement |
| A | 8 | 12 | 43 |
| B | 8 | 17 | 51 |
| C | 9 | 11 | 42 |
| D | 3 | 7 | 21 |
| E | 4 | 11 | 31 |
The variograms of the depth to the basement of the aquifer are shown for different zones in Figures 5 A, B, C, D and E. Figure 6A shows the mean variogram for the entire aquifer and Figures 6 B and C show the directional variograms of the variable. All the variograms show a nugget effect. However, if we analyze variograms in zones A (Figure 5 A) and C (Figure 5 C), they show clearly a sill value and their range can be inferred (a value of 12 km may approximately be taken), compared to the variogram in zone B ( Figure 4 B), D (Figure 4 D) and E (Figure 4 E) which show a pure nugget effect without giving any idea of a definite sill or range. This clearly shows the lack of correlation due to structural discontinuities in the zones B, D and E. Also, the directional variogram calculated in the direction 110 degrees taking values from the entire area, gives a variogram with a nugget effect, sill and range compared to the variogram calculated in the perpendicular direction (20 degrees) which gives a pure nugget effect only.
A similar exercise was carried out for transmissivity values. However, as the number of available T values was very small (Table 1), no meaningful variogram could be generated, even in zones A and C.
CONCLUSION
Modeling an aquifer in a hard rock region is not as straightforward as in a porous medium due to the highly variable and anisotropic medium. Discretization of the medium to use a finite difference approximation of the flow equation and the assignment of various parameters should be done using geological soft data available. The present study starts with the known lineaments and shows entirely the different variability of the same parameter in different zones demarcated by absence or presence of lineaments. It, therefore, becomes essential to perform such an exercise e.g., variographic analysis, by dividing the aquifer into sub-regions while studying such aquifers. The purpose of this study is to prove that if we perform a few trials by changing the region's boundary, we may arrive at the zones with and without hidden geological structures. Since the transmissivity values were available at a very few wells, the data could not give a reliable variability of the parameter to analyze the variogram.
However, water-table measurements clearly show significant changes in different zones and anisotropic behavior. Based on the regions marked by the variogram analysis, an aquifer may be realistically discretized and simulated. The calibration of parameters may be performed with low tolerance in the high variability zones.
REFERENCES
Aboufirassi, M. and M.A.Marino, (1984) Cokriging of Aquifer Transmissivity from Field Measurements of Transmissivity and Specific Capacity, J. Math. Geol. 16(1), p. 19-35.
Ahmed, S. (1985), Analyse statistique de quélques variables hydrogéologiques, D.E.A. dissertation (CFSG S-184), Ecole de Mines de Paris, France.
Ahmed, S. (1993) PLAYG: An interactive graphic software for simultaneous computation and modeling of an experimental variogram: A user's guide, NGRI, Hyderabad.
Ahmed, S. (1989) Geostatistics in aquifer parameter estimation: Some case studies. In proc. of Australian Workshop on Geostatistics in Water Resources, November 1989, Vol. 2, p. E1-20.
Gupta, C.P. and S. Sankaran (1986) Aquifer simulation in Vaippar basin. Tamilnadu, India, Tech. Rep. NGRI-86- Environ-13.
Marsily, G. de (1986) Quantitative Hydrogeology: Groundwater Hydrology for Engineers, Academic Press.
Marsily, G. de and S. Ahmed (1987) Application of Kriging Techniques in Groundwater Hydrology, Geol. Soc. India, Vol. 29(1), p.51-82.
Matheron, G. (1971) The theory of regionalized variogram and its application. C.G.G.M. doc. No.5, Ecole des Mines, Fontainebleau, France.
S. Sankaran
National Geophysical Research
Institute
Uppal Road, Hyderabad-50007, India
 Return to HydroWeb Homepage
Return to HydroWeb Homepage